Effect of Fees on Loan Rates (and nuance in APR)

 I was recently considering taking out a personal loan of £25,000 for a period of 4 years. I had two options:

• Loan offered at 2.84% interest rate, APR 2.84%
• Loan offered at 1.4% with a fees of £717, APR 2.84%

Which of the two is better? In UK, the standard way of comparing loans is APR. The Annual Percentage Rate (APR) is defined as the cost you pay each year to borrow money, including fees, expressed as a percentage. Since it is mandated by the FCA to include APR in all marketing and sales materials, this is what companies use either in their offering/advertisement, or as a subtext to the offering/advertisement.

To calculate this, the lender adds up the total costs, including fees, brokerages and interest and then calculates the effective rate charged to you, in the form of an annualised rate and share it with you. APR is calculated for the entire term of your loan. 

Note that the lender is charging you the fees upfront, while the interest is charged on the outstanding principal each month. If you decide to close the loan upfront, you still have to pay the fees in full. In the latter case (Loan offered at 1.4%, with a fees of £717, APR 2.84%), the lender is giving you £25,000, but the outstanding principal on day 0, i.e. the day the loan is issued, is actually $25,717, as the fees become due the day the loan is issued. You are then paying back £25,717 over the period of the loan at whatever is the actual rate of interest, in this case 1.4%. 

This is where I see a little issue with APR. If you take a loan of 48 months, and pay it off in exactly 48 months as per the agreed schedule, then all is well and comparing loans by APR makes sense. For instance, the two loan options I have above are exactly the same if I indeed pay them through the pre-agreed schedule.

However, if I want to pay the loan off after a year, then in the first case, my outstanding principal is £19,014 whereas in the second case, the outstanding principal is £19,422, though I have paid the same number of equated instalments each month thus far. This is because even though the interest rate is lower in the second case, the fees (not paid off thus far) far outweighs the lower interest thus far. 

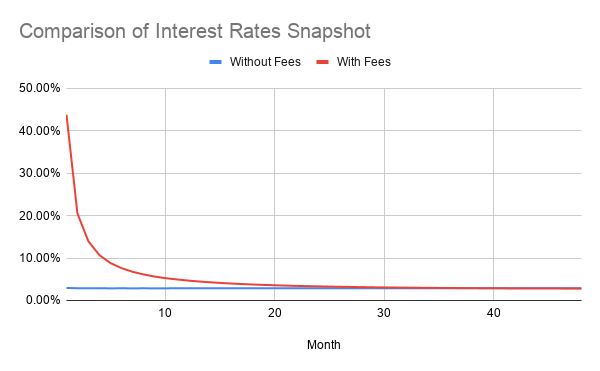
I present here the table of how this pans out for a few select periods:

	With Fees		Without Fees
At end of Month	Outstanding Principal	Snapshot of Interest Rate	Outstanding Principal	Snapshot of Interest Rate
1	$25,196.27	43.81%	$24,507.60	2.96%
6	$22,580.97	7.66%	$22,028.06	2.88%
12	$19,422.43	4.72%	$19,013.62	2.88%
24	$13,038.66	3.33%	$12,854.83	2.88%
36	$6,564.94	2.94%	$6,518.66	2.88%
48	$0.00	2.84%	$0.00	2.88%

The snapshot of interest rate indicated here is the interest rate you would have paid the lender over the period the loan was active, if you close your loan at that point by paying the outstanding loan, calculated as an annualised rate. As you can see, it starts very high for the case with fees and then slowly decreases ending up the same as the case without fees. Plotted as a graph, this is how the two snapshots chart:

In case of this particular personal loan, it is obvious that the offering without fees is far superior, as the interest I pay is the same, but it also gives me the optionality of paying off the loan sooner and not get penalised for doing so.

Now, in isolation, this analysis is interesting. However, personal loans are something most of us don't take that often, and even if we do, we generally intend to pay it off through the schedule - the upside of the paying it off sooner almost doesn't exist, specially at these low interest rates. 

There is another category of loans a lot of us take and one where we tend of pay off sooner than the intended duration - home loans. Every time we renegotiate the outstanding loan, after the fixed interest phase of 2 or 5 years are over, we are in effect borrowing from the new lender to pay off the old lender. Since the home loan sticks with us for the next 25-35 years, we often end up repaying the loan anywhere between 5-17 times. So, the effect of product fees can be massive. How so? Let's calculate.

Turns out, the effect of the fees can be rather extensive. Here is a comparison of a few specific cases I picked out:

	Live	Case 1	Case 2	Case 3
Loan Amount	£500,000	£500,000	£500,000	£200,000
Product Fees	£1,000	£2,000	£1,000	£2,000
Rate of Interest	1.40%	1.40%	1.40%	1.40%
Loan Duration (in years)	30	30	30	30
Advertised APR	1.42%	1.44%	1.42%	1.48%
Effective APR if renegotiated in 2 years	1.52%	1.62%	1.52%	1.94%
Effective APR if renegotiated in 5 years	1.45%	1.50%	1.45%	1.63%

As you can notice, the effective APR if renegotiated in a few months times is higher than the Rate of Interest as well as the advertised APR, and proportionally increases with the fees. The effect is much steeper with lower loan amounts, as the fees is a much bigger proportion of the loan amount. 

Next time you are offered loan choices, with and without fees, but with the same APR, use this structure to compare which one works out better for you. This is not an easy calculation, but fret not, I am sharing the sheet in which I did these calculations - you can copy the sheet and play around with the numbers for the specific offers you have at hand.

Disclaimer: Anything mentioned in this post should not be considered financial advice. The post should be consumed purely for entertainment and educational purposes.